Area Lights with LTCs

Bin­ary Re­flect­ance Dis­tri­bu­tion Func­tions

When shad­ing a point on a sur­face, phys­ic­ally, you need to take all in­com­ing rays from every dir­ec­tion in­to ac­count. Some light rays af­fect the fi­nal col­or of the shaded point more than oth­ers — de­pend­ing on their dir­ec­tion, the view dir­ec­tion and the prop­er­ties of the ma­ter­i­al.

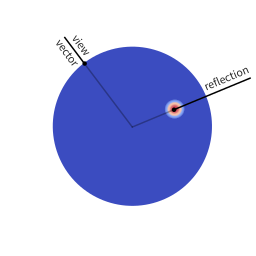
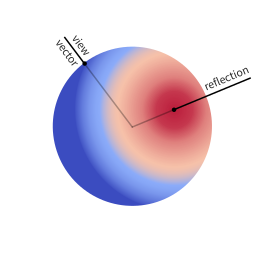
A per­fect mir­ror, for ex­ample, may take only the ex­act re­flec­tion of the view vec­tor in­to ac­count, as can be seen in fig­ure (a), where­as a more dif­fuse ma­ter­i­al will be af­fected by all or most in­com­ing rays sim­il­arly or equally, as visu­al­ized in fig­ure (b).

These fig­ures show spher­ic­al dis­tri­bu­tions: ima­gine you want to shade a point on a sur­face (the point where the view vec­tor is re­flec­ted). Ima­gine a ray of light hit­ting this point, it will pierce through the colored sphere at some loc­a­tion. The col­or at that loc­a­tion on the sphere in­dic­ates how much this ray will af­fect the col­or of the sur­face point: the more red, the high­er the ef­fect.

The func­tion that de­scribes how much ef­fect an in­com­ing light ray has for giv­en view­ing and in­com­ing light angles, is called BRDF. This func­tion is very spe­cif­ic to every ma­ter­i­al. As this is very im­prac­tic­al for real-time ren­der­ing and art pipelines, it is com­mon to in­stead use a so called para­met­ric BRDF; a func­tion which is able to ap­prox­im­ate many dif­fer­ent BRD­Fs of dif­fer­ent ma­ter­i­als us­ing in­tu­it­ive para­met­ers, e.g. rough­ness or metal­ness.

There are many para­met­ric BRD­Fs out there: the GGX mi­cro­fa­cet BRDF, the Schlick BRDF and the Cook-Tor­rance BRDF. I re­com­ment play­ing around with them in Dis­ney’s BRDF Ex­plorer.

Shad­ing area lights

With point lights, shad­ing is really simple as you only have a single in­com­ing ray — as­sum­ing you do not want to take in­dir­ect rays in­to ac­count. You can get the ap­pro­pri­ate factor (of how much of that ray will be re­flec­ted in view dir­ec­tion) from the BRDF us­ing the view angle and light angle, mul­tiply that with the light in­tens­ity and that is already it.

With area lights, it is a lot more com­plic­ated, as you have an in­fin­ite amount of in­com­ing rays. The fi­nal in­tens­ity of the shaded point is the in­teg­ral over the BRDF in the do­main of the poly­gon of the light (which, pro­jec­ted onto the spher­ic­al dis­tri­bu­tion, is a spher­ic­al poly­gon).

This is a prob­lem, be­cause we do not have an ana­lyt­ic­al solu­tion to in­teg­rat­ing over ar­bit­rary spher­ic­al dis­tri­bu­tions. In­stead, such a solu­tion is known only for very spe­cif­ic dis­tri­bu­tions, the uni­form sphere or the co­sine dis­tri­bu­tion for ex­ample.

So, how can we still do it without rad­ic­ally ap­prox­im­at­ing the area light?

Lin­early trans­formed co­sines

The geni­us of the pa­per is that the au­thors real­ized they can trans­form spher­ic­al dis­tri­bu­tions us­ing lin­ear trans­forms (scal­ing, ro­ta­tion and skew­ing) and that this leaves the value of the in­teg­ral un­changed.

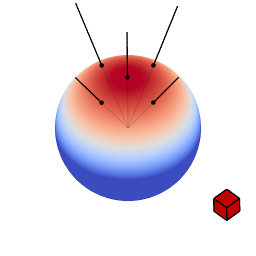
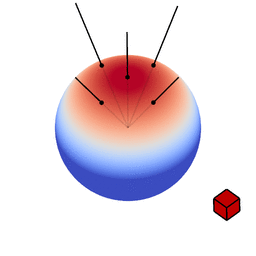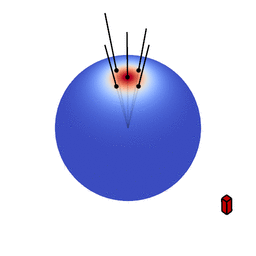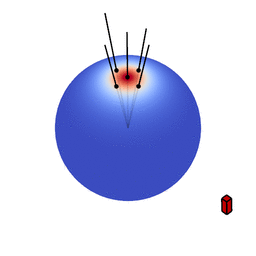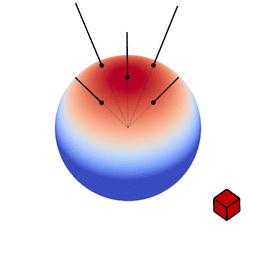
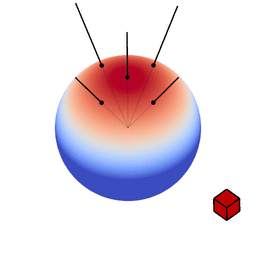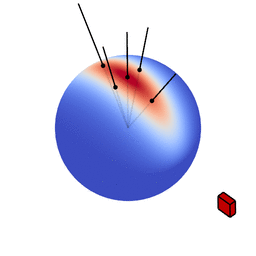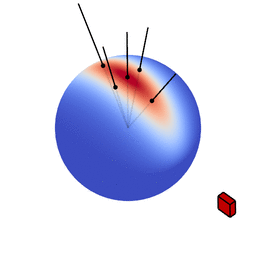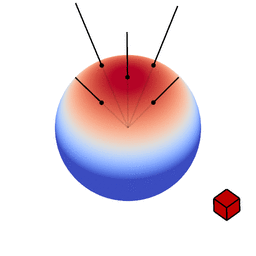
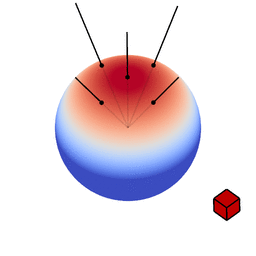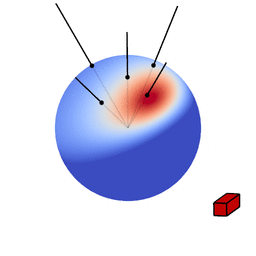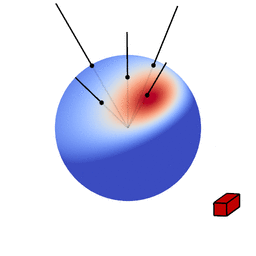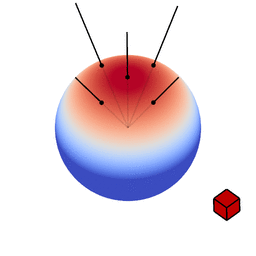
Im­age source: Eric Heitz’s Re­search Page

You can there­fore trans­form a spher­ic­al dis­tri­bu­tion to look like an­oth­er spher­ic­al dis­tri­bu­tion. This means that you can trans­form some­thing like the co­sine dis­tri­bu­tion to look like a spe­cif­ic BRDF giv­en a cer­tain view angle. You can then — be­cause the in­teg­ral is un­af­fected by the lin­ear trans­form — in­teg­rate over the co­sine dis­tri­bu­tion, to which an ana­lyt­ic­al solu­tion is known, in­stead of in­teg­rat­ing over the BRDF.

As this BRDF is view de­pend­ent, you need a trans­form­a­tion for every in­cid­ent view angle, and every para­met­er of a para­met­ric BRDF. In the pa­per, they achieve this by fit­ting a 3x3 mat­rix (for the trans­form­a­tion) for a set of sampled val­ues for the BRDF para­met­er alpha (rough­ness) of the GGX Mi­cro­fa­cet BRDF as well as the view­ing angle.

The 3x3 matrices have only four really sig­ni­fic­ant com­pon­ents. Con­sequently they can be stored in an RGBA tex­ture.

For shad­ing we need the in­verse matrices to trans­form the poly­gon of the light. Ori­gin­ally it is of course in the space of the BRDF over which we do not know how to in­teg­rate over. If we ap­ply the in­verse mat­rix to poly­gon, it is then in the space of the co­sine dis­tri­bu­tion over which we can in­teg­rate in­stead.

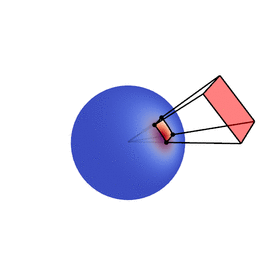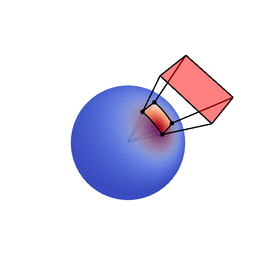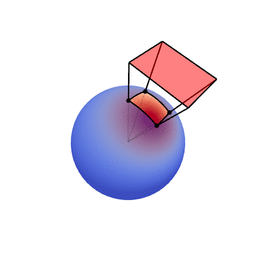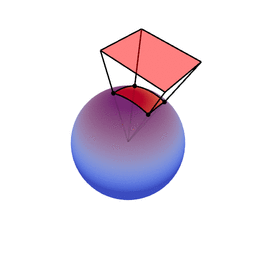
Im­age source: Eric Heitz’s Re­search Page

Load­ing LTC mat­rix tex­tures

The ori­gin­al C++ im­ple­ment­a­tion provided with the pa­per already con­tained .dds files for the fit­ted in­verse LTC matrices. Many thanks to Eric Heitz, who was kind enough to let me use these for the Mag­num ex­ample.

I packed these dds files as a re­source in­to the bin­ary (makes port­ing to web easi­er later). It was a mat­ter of simply adding the resources.conf, telling Cor­rade to com­pile it in your CMakeLists.txt…

corrade_add_resource(AreaLights_RESOURCES resources.conf)

add_executable(magnum-arealights AreaLightsExample.cpp ${AreaLights_RESOURCES})

… and then load­ing the tex­ture from the re­source memory us­ing DdsIm­port­er:

/* Load the DdsImporter plugin */
PluginManager::Manager<Trade::AbstractImporter> manager;
Containers::Pointer<Trade::AbstractImporter> importer =
    manager.loadAndInstantiate("DdsImporter");
if(!importer) std::exit(1);

/* Get the resource containing the images */
const Utility::Resource rs{"arealights-data"};
if(!importer->openData(rs.getRaw("ltc_mat.dds")))
    std::exit(2);

/* Set texture data and parameters */
Containers::Optional<Trade::ImageData2D> image = importer->image2D(0);
CORRADE_INTERNAL_ASSERT(image);
_ltcMat.setWrapping(SamplerWrapping::ClampToEdge)
    .setMagnificationFilter(SamplerFilter::Linear)
    .setMinificationFilter(SamplerFilter::Linear)
    .setStorage(1, GL::TextureFormat::RGBA32F, image->size())
    .setSubImage(0, {}, *image);

/* Bind the texture for use in the shader */
_shader.bindLtcMatTexture(_ltcMat);

Shader Hot-Re­load

Dur­ing shader de­vel­op­ment, you will not want to re­start your ap­plic­a­tion every time you make a change to the GLSL shader code. It is rather nice to be able to just hit F5 and see the changes im­me­di­ately in­stead.

It turns out that if you im­ple­men­ted an GL::Ab­stract­Shader­Pro­gram, hot-re­load­ing is just a mat­ter of re­in­stan­ti­at­ing it:

/* Reload the shader */
_shader = AreaLightShader{};

Yes, it is that simple.

Of­ten you will com­pile your shader files as re­sources in Mag­num (as done in the ex­ample). To use shaders from a re­source in your GL::Ab­stract­Shader­Pro­gram you would again make use of Util­ity::Re­source:

GL::Shader vert{version, GL::Shader::Type::Vertex};
GL::Shader frag{version, GL::Shader::Type::Fragment};

/* Load shaders from compiled-in resource */
Utility::Resource rs("arealights-data");
vert.addSource(rs.get("AreaLights.vert"));
frag.addSource(rs.get("AreaLights.frag"));

In this case you will need to over­ride the re­source group us­ing Util­ity::Re­source::over­ride­Group() to load the re­source from the ori­gin­al file rather than from memory be­fore hot-re­load­ing:

/* Reload the shader */
Utility::Resource::overrideGroup("arealights-data", "<path>/resources.conf");
_shader = Shaders::AreaLight{};